14 Dec 2021 — 4 minutes
Ambipolar diffusion in the lower solar atmosphere: MHD simulations of a sunspot
Conor D. MacBride1, David B. Jess1,2 and Elena Khomenko3,4
1Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, Belfast BT7 1NN, UK; 2Department of Physics and Astronomy, California State University Northridge, Northridge, CA 91330, USA; 3Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain; 4Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
This poster was presented at the AGU Fall Meeting 2021.
Abstract
Behind MHD is the assumption that there is a low degree of plasma ionization. However, in the upper photosphere and chromosphere a reduced temperature often results in the partial ionization of the plasma. The interaction between the decoupled neutral and ionized components of such a partially ionized plasma produce ambipolar diffusion. To investigate the role of ambipolar diffusion in energy transfer and dissipation in the chromosphere, we analyze a 2D numerical model of magnetoacoustic waves propagating through the chromosphere above the umbra of a sunspot. We solve the ideal MHD equations for perturbations to the magnetostatic equilibrium using the Mancha code. The effect of ambipolar diffusion is isolated by varying the inclusion of additional terms in the MHD equations which account for this process. Data-driven perturbations are introduced in the photosphere using observational SDO/HMI umbral velocity time series. Using energy spectra, we analyze the chromospheric dynamics of our simulation and gather insights into the role of ambipolar diffusion, and partial ionization, in energy transfer and dissipation in the lower solar atmosphere.
Introduction
The low degree of plasma ionization in the solar atmosphere can affect the plasma properties significantly. The abundance of neutral particles can result in additional physical processes, such as Hall diffusion, the Biermann battery effect and ambipolar diffusion.
When the neutral plasma component interacts with the ionized plasma component, which is manipulated by the magnetic field, the friction between the particles leads to the process of ambipolar diffusion. This study focuses on ambipolar diffusion occuring in the atmosphere above a sunspot’s umbra.
We use numerical MHD simulations to investigate the effect ambipolar diffusion has within the lower solar atmosphere above a sunspot.
Mancha3D Code
We use the Mancha3D code (Khomenko & Collados (2006); Felipe et al. (2010)) to solve the 3D nonlinear ideal magnetohydrodynamic (MHD) equations for perturbations to the magnetostatic equilibrium.
Mancha3D includes terms modeling ambipolar diffusion in the MHD equations, and optionally allows these terms to be excluded. The parameter controlling ambipolar diffusion is,
\(\eta_A = \dfrac{\xi_n^2 \vert\mathbf{B}\vert^2}{\alpha_n}\),
where \(\xi_n\) is the fraction of neutrals, \(\mathbf{B}\) is the magnetic field and \(\alpha_n\) is the neutral collisional parameter. Within the MHD equations, this term acts on the perpendicular component of the plasma current \(\mathbf{J}_\perp\).
Key Results
Two simulations are computed: one with ambipolar diffusion terms in the MHD equations, and one without. We compare the two simulations to see the effect of ambipolar diffusion and investigate the role it plays in the lower solar atmosphere.
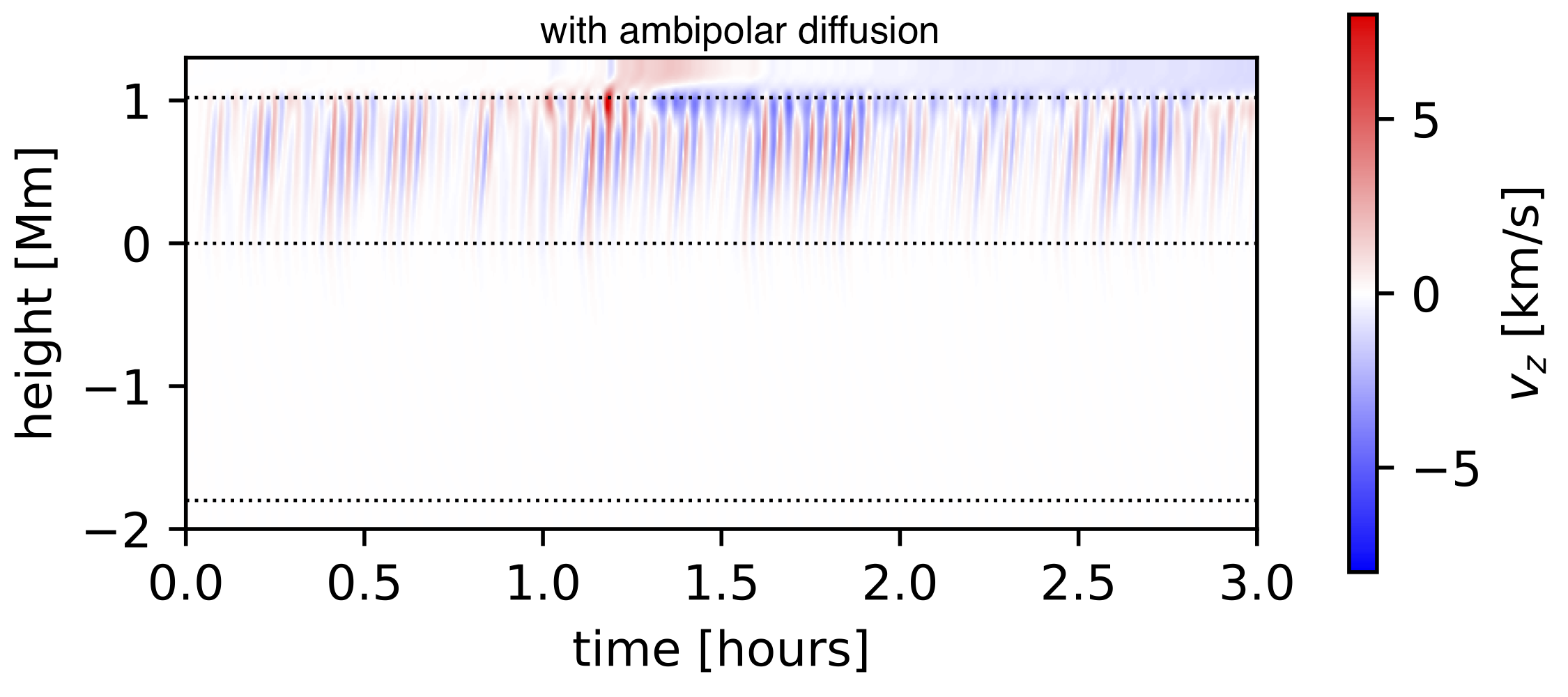
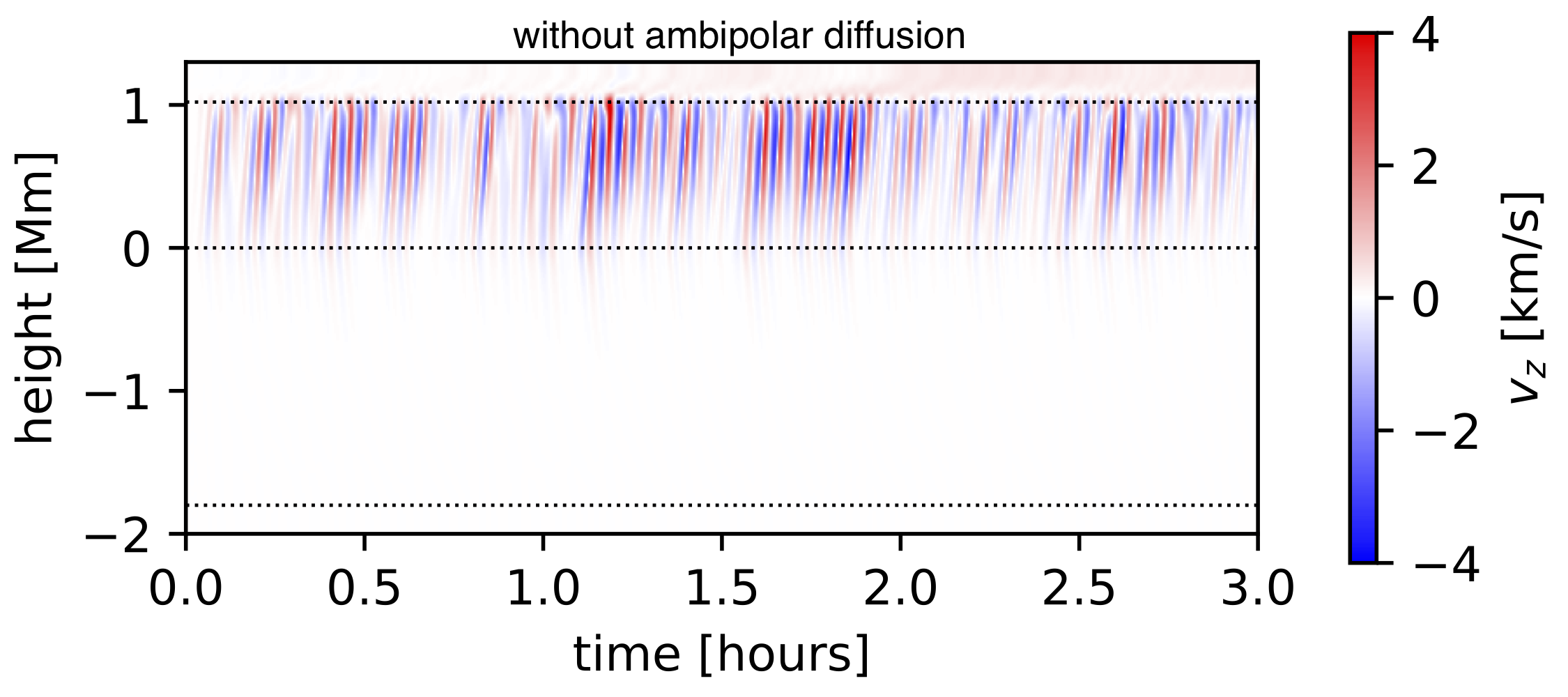
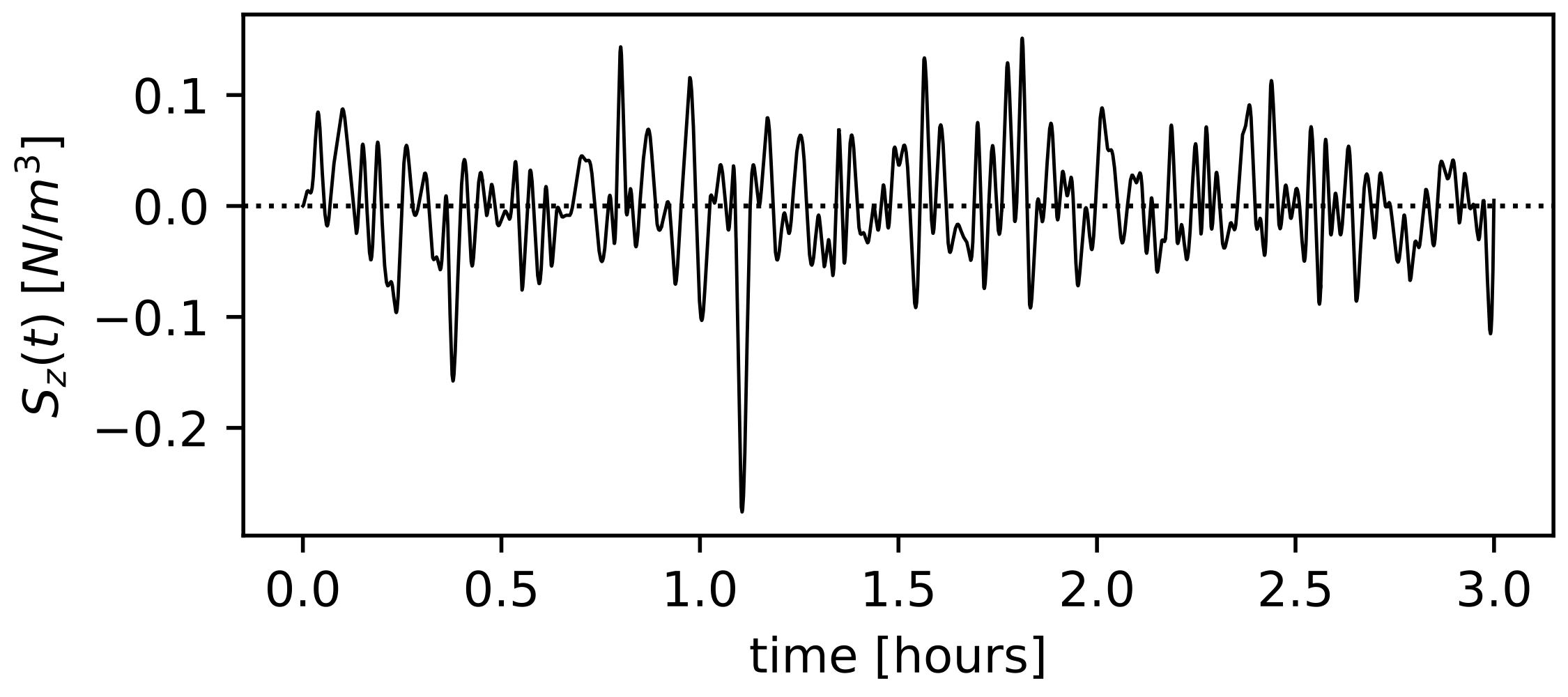
The simulations are run for a total of 3 hours each, with snapshots saved every 10 seconds. The plots above show the z component of velocity along the axis of the sunspot throughout time for both simulations.
Energy spectral densities are calculated for each simulation and at each atmospheric height along the axis of the sunspot. We measure the gradient (power law index) by fitting a power law to the spectral densities above the enhancement frequency of 6.1 mHz, as shown in the example plot below for the ambipolar diffusion simulation at photospheric height,
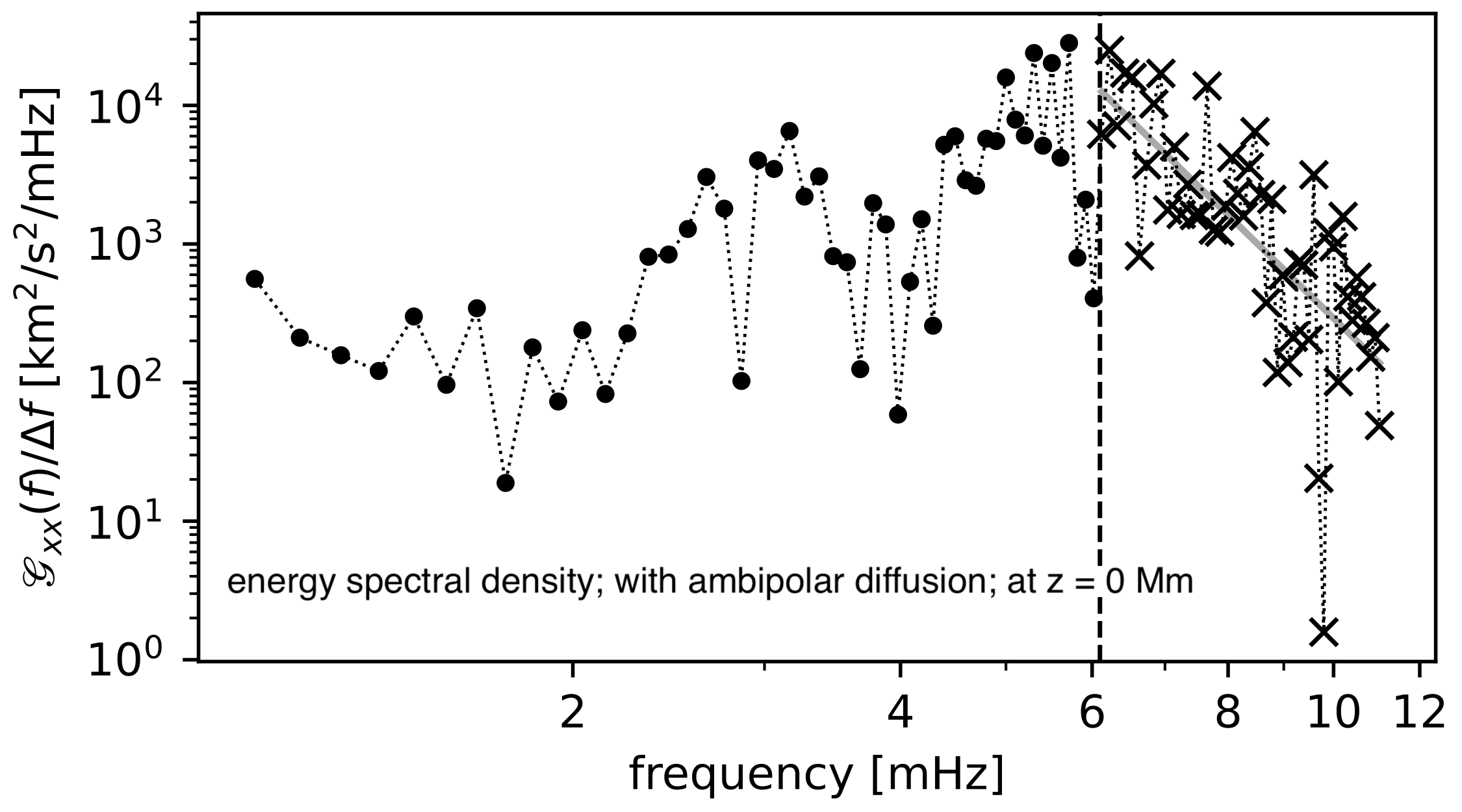
We focus our analysis at the atmospheric heights from 500 km to 1000 km as these heights are associated with wave activity pushing up from the mid-photosphere to the chromosphere (Prasad et al. (2017)). The power law indicies from the two simulations are plotted throughout this height range in the following plot,
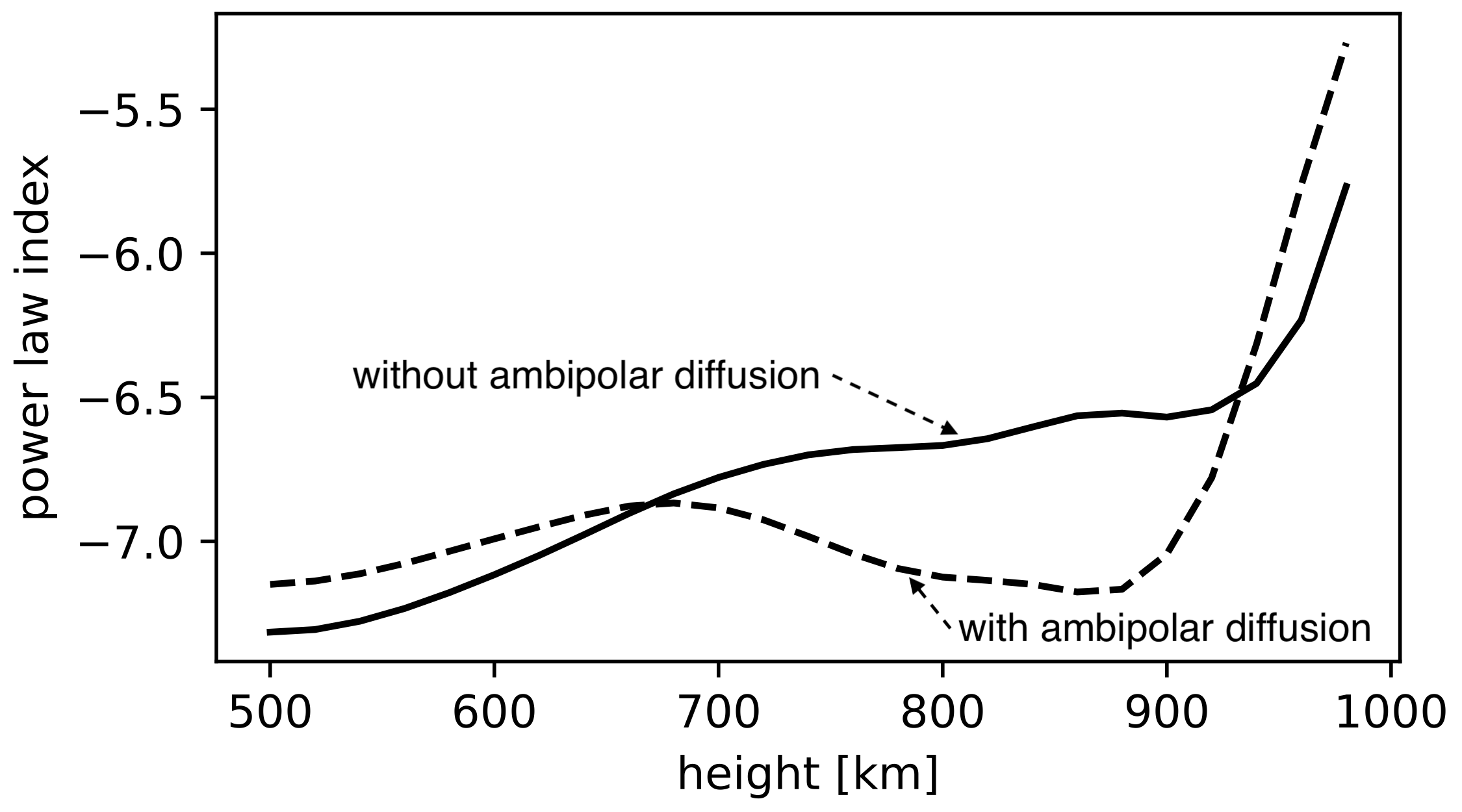
A decrease in power law index (steeper energy spectral density gradient) is observed in the ambipolar diffusion simulation between the heights of 680 km and 920 km.
Model Sunspot Atmosphere and Simulation Configuration
The sunspot model atmosphere is created according to Khomenko & Collados (2008). It is transformed to a 2D model in Cartesian coordinates centered along the axis of the sunspot, and adjusted to be convection-stable.
It is 13.2 Mm in the horizontal direction and 2.8 Mm in the vertical direction, with 1 Mm above the photosphere. Grid points are spaced 50 km along the horizontal and 20 km along the vertical. The time step is 0.008 seconds.
Periodic boundaries are used on the left and right, and perfectly matched layers (PMLs) are used on the upper and lower.
Perturbations are applied along the z-axis at photospheric height at the center of the sunspot. To use a realistic driver signature, amplitudes are extracted from Doppler velocity observations from HMI/SDO.
Summary
- Evaluated two MHD simulations of the atmosphere above a sunspot — with and without ambipolar diffusion.
- Analyzed and compared the energy spectral density of both simulations between the heights of 500 km – 1000 km.
- Significant difference between the power law indices of both simulations between the atmospheric heights of 680 km – 920 km.
References
- Felipe, T., Khomenko, E., & Collados, M. 2010, The Astrophysical Journal, 719, 357, doi: 10.1088/0004-637X/719/1/357
- Khomenko, E., & Collados, M. 2006, The Astrophysical Journal, 653, 739, doi: 10.1086/507760
- Khomenko, E., & Collados, M. 2008, The Astrophysical Journal, 689, 1379, doi: 10.1086/592681
- Prasad, S. K., Jess, D. B., Doorsselaere, T. V., et al. 2017, The Astrophysical Journal, 847, 5, doi: 10.3847/1538-4357/aa86b5
